Ch3-Rigid-Body Motions
Summary:
-
主要思想是用旋转或者变换矩阵来描述空间中构型之间的关系。
- 由于C-Space的非欧式空间属性,引入了Twist(Spatial Velocity)和Wrench(Spatial Force),通过对Twist的积分,能够得到一个沿着固定轴旋转平移的运动(Screw Motion),这种用六自由度描述运动的方式是我学习这本书的主要原因之一。Craig的机器人学导论中主要用DH参数计算变换矩阵,而exponential coordinates有其自己的优点(体现在正运动学的计算上,Product of exponentials 的计算更加的自由和简洁)
- 本章的重点围绕在李群和李代数上,旋转矩阵或者变换矩阵属于某一类李群,而对应的外积算子属于对应的李代数。之后的串联机械臂的运动学以此为基础,用矩阵的指数运算来提高计算精度以及计算的速度。同时矩阵的指数和对数计算能够更加方便和直观的求得对应的运动状态。
3.1. 平面内的运动和坐标变换
这部分是个引子,用来引出三维空间下的坐标变换矩阵。
【定义】:在本书中一般定义固定坐标系为{s},本体坐标系为{b},同时使用右手系
从s到b的变换矩阵(b相对于s)可以将b坐标系的轴表示为s的坐标来定义
\[p=p_1 \hat{x}_s + p_2 \hat{y}_s + p_3 \hat{z}_s \\ \hat{x}_b = r_{11} \hat{x}_s + r_{21} \hat{y}_s + r_{31} \hat{z}_s \\ \hat{y}_b = r_{12} \hat{x}_s + r_{22} \hat{y}_s + r_{32} \hat{z}_s \\ \hat{z}_b = r_{13} \hat{x}_s + r_{23} \hat{y}_s + r_{33} \hat{z}_s \\\]那么在s坐标系下的一个向量p可以写成矢量形式,并且得到R矩阵(b坐标系以s坐标系为参考的旋转矩阵)
\[p=\begin{bmatrix} p_1 \\ p_2 \\ p_3 \end{bmatrix} \\ R_{sb}\to [\hat{x}_b,\hat{y}_b, \hat{z}_b]= [\hat{x}_s,\hat{y}_s, \hat{z}_s]\begin{bmatrix} r_{11},r_{12},r_{13}\\r_{21},r_{22},r_{23}\\r_{31},r_{32},r_{33}\\ \end{bmatrix} \\ [\hat{x}_b,\hat{y}_b, \hat{z}_b] ~_bp_{A} = [\hat{x}_s,\hat{y}_s, \hat{z}_s] R_{sb} ~_bp_{A} \\ \to _sp_{A} = R_{sb} ~_bp_{A}\]这里我的记忆方式是如果要写出从s到b(b相对于s)的矩阵,将b的每个轴(单位向量)用s坐标系表示为各自的列向量,然后排列成R矩阵即可。
思路2:R矩阵本身代表的就是两个body的变换
\[frame_{s} = \{\hat{x}_s,\hat{y}_s,\hat{z}_s\} \\ frame_{b} = \{\hat{x}_b,\hat{y}_b,\hat{z}_b\} \\ R_{bs}frame_{s} = frame_{b}\to R_{sb} = R_{bs}^T\]3.2. 旋转和角速度
旋转矩阵的9个变量中包含6个约束,可以是b坐标轴的单位长度以及各个轴之间正交,更简单的说就是(针对右手系):
\[detR=1\]三维空间下的旋转矩阵的集合被称为特殊正交群,也即SO(3),SO(n)群里的A, B满足以下的特征:
- 乘法封闭:AB属于该群
- 结合律:(AB)C=A(BC)
- 特殊元素:AI = IA
- 可逆:A * inv(A) = inv(A) * A = I
旋转矩阵的应用
- 表达一个姿态
- 改变一个向量或者坐标系所在的参考坐标系
- 根据该旋转操作旋转向量和坐标系
R和旋转轴所在的坐标系有关系
\[R_{sb'}=rotate\_by\_R\_in\_[s]\_frame (R_{sb}) = RR_{sb} =R_{rot\to b'}R_{sb}~~[premultiplying] \\ R_{sb''}=rotate\_by\_R\_in\_[b]\_frame (R_{sb}) = R_{sb}R=R_{sb}R_{bb''}~~~~~~[postmultiplying]\]旋转一个向量,因为这时只有一个固定坐标系:
\[v_{after\_rot}=Rv_{ini}\]角速度和旋转矩阵的关系
根据角速度到位置坐标的外积关系:
\[\dot{r_i} = \omega_s \times r_i, i = x,y,z\]而三个坐标轴向量恰好组成了旋转矩阵:
\[\dot{R} = \begin{bmatrix}\omega_s \times r_x & \omega_s \times r_y & \omega_s \times r_Z \end{bmatrix} = \omega_s \times R\]将向量叉乘符号写作矩阵形式(skew Symmetric)
\[[\omega_s]= \begin{bmatrix} 0 & -\omega_3, & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix}\]满足反对称阵的性质:
\[[\omega_s] = -[\omega_s]^T\]给定旋转轴向量以及旋转矩阵,成立:
\[R[\omega]R^T=[R\omega] \\ prove:\\ R^T=\begin{bmatrix}r_x^T\\r_y^T\\r_z^T \end{bmatrix}\\ [\omega]R=[\omega \times r_x,\omega \times r_y,\omega \times r_z] \\ R^T[\omega]R=\begin{bmatrix} r_x^T(\omega \times r_x) & r_x^T(\omega \times r_y) & r_x^T(\omega \times r_z)\\ r_y^T(\omega \times r_x) & r_y^T(\omega \times r_y) & r_y^T(\omega \times r_z)\\ r_z^T(\omega \times r_x) & r_z^T(\omega \times r_y) & r_z^T(\omega \times r_z) \end{bmatrix}\\ =\begin{bmatrix} 0 & -r_z^T \omega & r_y^T\omega \\ r_z^T \omega & 0 & -r_x^T\omega \\ -r_y^T \omega & r_x^T\omega & 0 \end{bmatrix}\\ \nearrow a\bullet(b\times c)=b\bullet(c\times a)=c\bullet(a\times b) \\ =[R^T\omega]\\ \nearrow R,R^T \in SO(3) \to Q.E.D.\\ \therefore \dot R= \omega_s \times R = [\omega_s]R \to [\omega_s]=\dot R R^{-1}\\ \omega_b=R_{sb}^{-1}\omega_s=R^{-1}\omega_s=R^T \omega_s\\ \to [\omega_b]=[R^T \omega_s]=R^T[\omega_s]R=R^T(\dot R R^T)R=R^T \dot R=R^{-1} \dot R\]注意:两个角速度只和自己的下标坐标系有关,和另外一个坐标系是独立的。
(此处留空:现在貌似并不知道用R来表示角速度有什么用??以后回来再写吧)
旋转矩阵的指数坐标表示
这部分很简单,对指数进行泰勒展开即可。
\[e^{at}=1+at+\frac{(at)^2}{2!}+\frac{(at)^3}{3!}+...\]对矩阵也同样有这种形式:
\[e^{At}=I+At+\frac{(At)^2}{2!}+\frac{(At)^3}{3!}+...\\ =I+(PDP^{-1})t+(PDP^{-1})(PDP^{-1})\frac{t^2}{2!}+...\\ =P(I+Dt+\frac{(Dt)^2}{2!}+...)P^{-1}\\ =Pe^{Dt}P^{-1}\\ \nearrow(A=PDP^{-1},)\]指数坐标下的旋转表示
绕旋转轴转动的向量p的速度之前表示为外积的形式:
\[\dot p=\hat{\omega}\times p=[\hat{\omega}]p\to p(t)=e^{[\hat{\omega}]t}p(0)=p(\theta)\nearrow \dot \theta=1\]对指数进行泰勒展开
\[[\hat{\omega}]^3=-[\hat{\omega}]\to [\hat{\omega}]^5=[\hat{\omega}]\\ e^{[\hat{\omega}]\theta}=I+(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-...)[\hat{\omega}]+(\frac{\theta^2}{2!}-\frac{\theta^4}{4!}+\frac{\theta^6}{6!}...)[\hat{\omega}]^2\\ \to Rot(\hat{\omega},\theta)=I+sin\theta[\hat{\omega}]+(1-cos\theta)[\hat{\omega}]^2\in SO(3)\]我们这里就推导得出了经典的罗德里格旋转公式(广泛应用于坐标变换)
这里依然可以对比两个公式:
\[R'=e^{[\hat{\omega}]\theta}R=Rot(\hat{\omega},\theta)R ~~~... fixed~frame\\ R''=R e^{[\hat{\omega}]\theta}=RRot(\hat{\omega},\theta) ~~~...body~frame\\\]第一个Rot在左边表示一个旋转操作,是在固定坐标系下操作的。第二个Rot在右边相当于在R的坐标系中找旋转轴,按照自身的轴转动。
需要区分二者的不同,很多地方都会涉及到和这个类似的参考系的选取问题。
旋转矩阵的指数和对数操作
既然SO3下的旋转矩阵可以用so3的指数形式求得,那么对SO3求对数应该也可以反推so3下的旋转轴以及角度
这里对含有三角函数以及旋转轴的矩阵中的项进行变换:
\[r_{32}-r_{23}=2\hat{\omega}_1sin{\theta}\\ r_{13}-r_{31}=2\hat{\omega}_2sin{\theta}\\ r_{21}-r_{12}=2\hat{\omega}_3sin{\theta}\\ \to \\ [\hat{\omega}]=\frac{1}{2sin\theta}(R-R^T)\]如何从R求旋转角?从矩阵的迹可以发现:
\[tr{R}=r_{11}+r_{22}+r_{33} = 1+2cos\theta \nearrow ||\hat{\omega}||_2=1\]只要当旋转角度不是π的倍数时,从旋转矩阵可以唯一求出旋转角度和旋转轴:
特殊情况:
- R=I,此时角度为0,旋转轴没有定义
- trR=-1,此时角度为pi,但是旋转轴有多个可行解:
\[\hat{\omega}=\frac{1}{\sqrt{2(1+r_{33})}}\begin{bmatrix}r_{13} \\ r_{23} \\ 1+r_{33}\end{bmatrix}, \frac{1}{\sqrt{2(1+r_{22})}}\begin{bmatrix}r_{12} \\ 1+r_{22} \\ r_{32}\end{bmatrix}, \frac{1}{\sqrt{2(1+r_{11})}}\begin{bmatrix}1 + r_{11} \\ r_{21} \\ r_{31}\end{bmatrix},\\-\hat{\omega} ~is~also~ok!\]
- 其他情况:
\[\theta=cos^{-1}((trR-1)/2)\in[0,\pi)\to [\hat{\omega}]=\frac{1}{2sin\theta}(R-R^T)\]
因为旋转轴的范数小于1,并且转动角度范数小于pi,因此可以画出旋转矩阵的群SO3到一个半径为pi的球上,在这种假设下,其实可以得到改进的罗德里格参数。
(貌似这里的旋转轴和欧拉角一样也存在奇异性?欧拉角的万向节死锁,罗德里格参数也有切坐标的问题)
刚体运动和Twist!
主要讲SE(3)和se(3)的关系,和前面大同小异。
齐次变换矩阵或者说是刚体运动的群,定义为特殊欧式群:
\[T=\begin{bmatrix}R_{3\times 3} & p_{3\times 1}\\0 & 1\end{bmatrix}\]对于SE(3),因为含有SO(3)的子矩阵,有如下的性质:
- 可逆
- 乘法封闭
- 结合律
欧式空间下的坐标变换,此时向量x扩充为一个四元向量,只不过最后一位始终为1:
\[Tx'=T\begin{bmatrix}x \\1 \end{bmatrix} =\begin{bmatrix}Rx+p \\1 \end{bmatrix}\]并且齐次变换T不改变向量的二范数大小,和内积。
和旋转变换相似,齐次变换矩阵T也有三个功能
- 表示一个刚体的构位,位置和姿态
- 改变一个向量或者坐标系的参考系
- 去移动一个向量或者坐标系
其中表示移动操作时也有参考系选取的问题:
\[T_{sb'} = TT_{sb} = \{Trans(p)Rot(\hat{\omega},\theta)\}T_{sb}~~~...Fixed~Frame\\ T_{sb''} = T_{sb}T = T_{sb}\{Trans(p)Rot(\hat{\omega},\theta)\}~~~...Body~Frame\]Twists(扭转速度)
从之前角速度的斜对称阵和旋转矩阵和其导数的关系,我们可以想到SE(3)下的变换阵是否也有这种操作:
\[T^{-1}\dot{T}=\begin{bmatrix}R^T & -R^Tp\\0 & 1\end{bmatrix}\begin{bmatrix}\dot R & \dot p\\0 & 0\end{bmatrix} \\ =\begin{bmatrix}R^T \dot R & R^T \dot p\\0 & 0\end{bmatrix} \\ =\begin{bmatrix}[\hat{\omega}_b] & v_b \\0 & 0 \end{bmatrix}\]还是要注意参考系的问题,这里的下标b表示这个矩阵表示的是运动的坐标系相对于此时body上静止参考系的速度和角速度。同时我们也发现将角速度和速度写在一起是合理的,能够表示刚体的运动状态:
body坐标系下的空间速度(Spatial Velocity),或者简称为body twist:
\[\mathcal{V}_b=\begin{bmatrix}\omega_b \\ v_b \end{bmatrix}\]然后就能导出se(3)和SE(3)的关系:
\[T^{-1}\dot{T} = [\mathcal{V}_b]=\begin{bmatrix} [\omega_b] & v_b \\ 0 & 0 \end{bmatrix}\]这是其物理解释,我们也可以解释另外一个twist的含义:
\[\dot T T^{-1}=\begin{bmatrix}\dot R & \dot p\\0 & 0\end{bmatrix} \begin{bmatrix}R^T & -R^Tp\\0 & 1\end{bmatrix}\\ =\begin{bmatrix}\dot R R^T & \dot p - \dot R R^T p\\0 & 0\end{bmatrix} \\ =\begin{bmatrix}[\hat{\omega}_s] & v_s \\0 & 0 \end{bmatrix}\]这里的vs并不是body frame在固定坐标系下的速度(\dot p),而是
\[v_s=\dot p + \omega_s \times (-p)\]这里vs的物理意义应该解释为,body本身是个无穷大的刚体,vs的body上任意一点相对于s的速度。
-
并且wb是在b系下的角速度,ws是s系下的角速度。
-
vb是b原点在b坐标系下的线速度,vs是s的原点重合在b上某一点在s坐标系下的线速度
并且\mathcal{V}_b和\mathcal{V}_s可以互相转换:
\[[\mathcal{V}_b]=T^{-1}\dot T=T^{-1}[\mathcal{V}_s]T\\ [\mathcal{V}_s]=\dot T T^{-1}=T[\mathcal{V}_b]T^{-1}\\\]对[vs]展开:
\[[\mathcal{V}_s]=\begin{bmatrix}R[\omega_b]R^T & -R[\omega_b]R^Tp+Rv_b \\ 0 &0\end{bmatrix}=\begin{bmatrix}[R\omega_b] & -[R\omega_b]p+R v_b \\0 & 0\end{bmatrix} \\ =\begin{bmatrix}[R\omega_b] & [p]R\omega_b+R v_b \\0 & 0\end{bmatrix} \\ \to \mathcal{V}_s=\begin{bmatrix}\omega_s \\ v_s\end{bmatrix} = \begin{bmatrix}R & 0 \\ [p]R & R\end{bmatrix} \begin{bmatrix}\omega_b \\ v_b\end{bmatrix}\]这里的6x6矩阵在处理twist的坐标上有很好的作用,给它单独起个名字adjoint map。
\[[Ad_T]=\begin{bmatrix}R & 0 \\ [p]R & R\end{bmatrix} \in \R^{6\times6}\]T的下标和旋转矩阵R的下标相同,性质也类似。
Twist的旋量表达
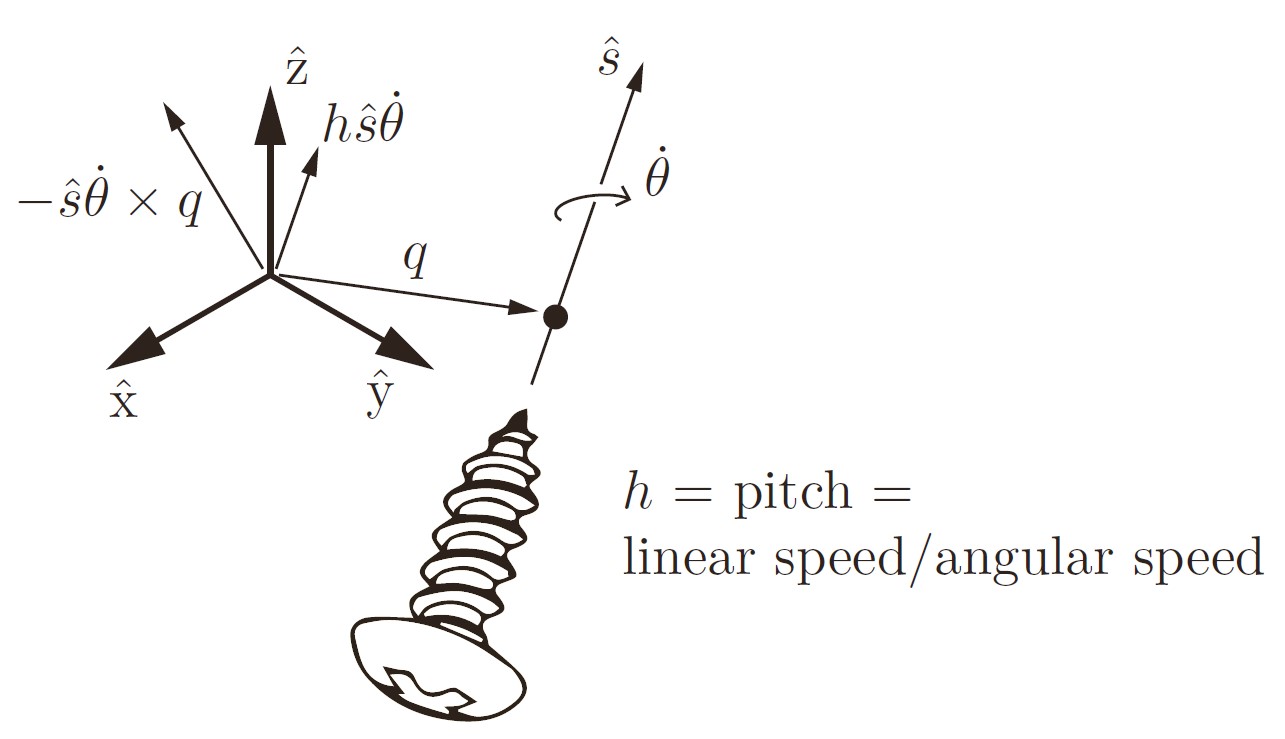
简单的说,旋量包含一个点q,一个单位长度的旋转轴方向\hat{s}以及所谓的螺距(线速度/角速度)
我们可以吧之前的空间旋转速度twist转化为对应的绕旋量S并且有角速度\dot{\theta}的运动:
\[\mathcal{V}=\begin{bmatrix} \omega \\ v \end{bmatrix} =\begin{bmatrix} \omega \\ -\omega \times q + \dot{q} \end{bmatrix} = \begin{bmatrix} \hat{s}\dot{\theta} \\ -\hat{s}\dot{\theta} \times q + h \hat{s} \dot{\theta}\end{bmatrix}\]其中速度的分量包含原点绕轴转动的线速度以及本体的速度两部分。
因为\hat{s}是单位向量,因此可以得到:
\[\hat{s} = \frac{\omega}{||\omega||},\dot \theta=||\omega||,h=\frac{\hat{\omega}^Tv}{\dot{\theta}}\]并且q是满足
\[\hat{s}\dot{\theta} \times q=h\hat{s}\dot{\theta}-v\]的线性方程的解。
这个定义当角速度为0时,需要修改,此时h是无穷大,旋量仍然是单位向量,只不过和线速度方向相同,此时的\dot{\theta}代表线速度的大小。
为了避免h无穷大的情况,我们用twist的归一化版本来定义旋转轴S
- 角速度不为0
- 角速度为0
归一化之后的S仍然有运算符使其满足se(3):
\[[S]=\begin{bmatrix}[\omega] &v\\0 & 0 \end{bmatrix} \in se(3),~~ [\omega]=\begin{bmatrix} 0 & -\omega_3, & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix} \in so(3)\]由于是twist的归一化变量,因此也满足Adjoint的变换形式:
\[S_a=[Ad_{T_{ab}}]S_b\]刚体运动的指数/对数变换
根据 Chasles-Mozzi 理论每一次刚体的运动都可以表示为沿空间中screw axis(单位向量)旋转\theta
\[exp:[S]\theta\in se(3) \to T \in SE(3) \\ log:T \in SE(3) \to [S]\theta\in se(3) \\\]指数形式和SO(3)的很相似:
\[e^{[S]\theta}=I+[S]\theta+[S]^2 \frac{\theta^2}{2!}+... \\ =\begin{bmatrix} e^{[\omega]\theta} & G(\theta)v \\ 0 & 1 \end{bmatrix} \\ G(\theta) =0 + \theta + [\omega] \frac{\theta^2}{2!} + [\omega]^2 \frac{\theta^3}{3!} + ... \\ =I\theta+(1-cos(\theta))[\omega] +(\theta - sin(\theta))[\omega]^2\]\[G(\theta) 和Rot(\omega,\theta)不一样!!!\]
如果角速度为0,则可以表示为:
\[e^{[S]\theta}=\begin{bmatrix} I & v \theta \\ 0 & 1 \end{bmatrix} \\ G(\theta) = \theta, R = I\]对应的对数形式:
只要一一对应矩阵中的元素:
\[G(\theta) v =p\to v = G^{-1}(\theta) p\\ G^{-1}(\theta) = I/\theta - [\omega] / 2 + (1/\theta - cot(\theta/2)/2) [\omega]^2\]Wrenches
讲完了速度,该讲力了,这里的力指的是包含力(force)和力矩(moment):
\[\mathcal{F}=\begin{bmatrix} m_a \\ f_a\end{bmatrix}\]wrenches也可以在不同的坐标系下切换,准则是功率不变!:
\[\mathcal{V}_b^T\mathcal{F}_b=\mathcal{V}_a^T\mathcal{F}_a =([Ad_{T_{ab}}]\mathcal{V}_b)^T\mathcal{F}_a=\mathcal{V}_b^T[Ad_{T_{ab}}]^T\mathcal{F}_a \\ \to \mathcal{F}_b=[Ad_{T_{ab}}]^T\mathcal{F}_a\\ \to \mathcal{F}_a=[Ad_{T_{ba}}]^T\mathcal{F}_b\\\]注意这里的下标方向!!!
例子和作业
暂时不想更了…头痛…
觉得这块主要是概念,其次才是计算,做第二次作业再来更新这块吧。