Ch8-Dynamics of Open Chains-Part1, Inverse Dynamics
Summary:
-
机器人的动力学我暂时先分成两部分,第一部分是逆动力学,第二部分是正向动力学。所谓正逆,可以这么理解,对于动力学公式的\tau= f(\theta, \dot\theta, \ddot\theta),人们从当前系统的输入:\tau以及当前机器人的状态\theta, \dot\theta 可以推算出此时系统的\ddot \theta,这一过程是正向的,因此被称作Forward Dynamics。而该过程的逆过程,也就是已知当前的期望输出\ddot\theta和当前的状态,希望反向求出此时机器人应该输入的力矩\tau,就被叫做Inverse Dynamics。
- 因为推导逆动力学在实际中比较常用(根据规划的轨迹计算需要给机器人提供的力矩前馈),同时动力学公式也能看出FD比ID要多算一个质量矩阵的逆,因此我们先考虑ID的问题。
- ID的计算主要有两种方法:拉格朗日微分的方法和牛顿欧拉迭代的方法。前者在数学上比较的直观,但缺点也是因为要计算微分,所以目前计算机暂时没有高效推导的办法(就算推导出来也是一大堆符号公式);而牛顿欧拉的迭代方式是数值解法,对计算机来说非常友好,并且在时间复杂度上也是接近O(n*d)复杂度(n是tree所有节点的数量, d是树的深度),至于FD,因为如果直接求M的逆的话时间复杂度也会很高O(n^3)?Part2会介绍两种计算方法。
拉格朗日方法
拉格朗日的概念非常的简洁,并且非常适用于简单的低自由度(DOF <= 3)的机器人,但是自由度高了就推不动了…
该方法第一步就是建立互相独立的一系列广义坐标系:q\in \R^n,然后根据广义坐标系定义广义力 f \in \R^n。 然后根据虚功原理, f^T \dot{q} 对应功率。建立整个系统的能量(动能+势能)之后直接丢给拉格朗日方程就可以了,不用进行复杂并且容易出错的受力分析。
这里省略一万字关于拉格朗日方程和牛顿运动定律的等价关系,以及变分和最小作用量原理等等….[1]
总之就有了:
\[\mathcal{L}(q,\dot{q})=\mathcal{K}(q,\dot{q}) - \mathcal{P}(q) \\ f=\frac{d}{dt}\frac{\partial \mathcal{L}}{\partial \dot{q}} - \frac{\partial \mathcal{L}}{\partial q}\]当f=0时,就是对应的Euler-Largrange 方程。
简单例子: 2R机械臂
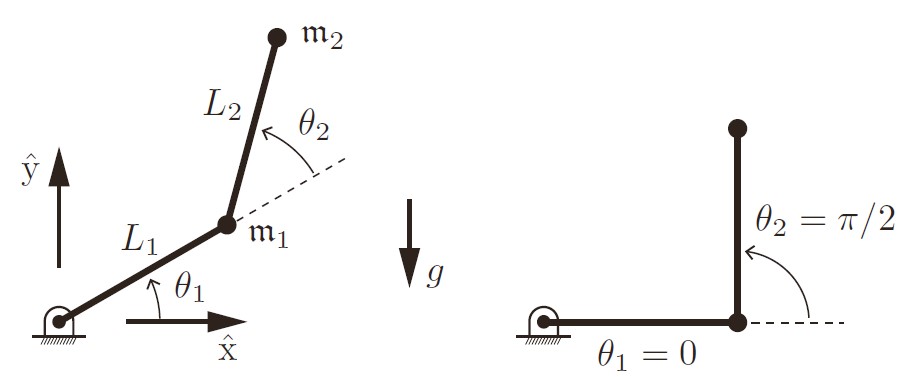
我们建立广义坐标系(极坐标),这样最终的f就是关于\theta状态的函数,也就是我们想要的ID的结果。
\[\begin{bmatrix}x_1 \\ y_1 \end{bmatrix} = \begin{bmatrix}L_1 cos(\theta_1) \\ L_1sin(\theta_1) \end{bmatrix} \\ \to \begin{bmatrix}\dot x_1 \\ \dot y_1 \end{bmatrix} = \begin{bmatrix}-L_1 sin(\theta_1) \\ L_1cos(\theta_1) \end{bmatrix} \dot{\theta} \\ \begin{bmatrix}x_2 \\ y_2 \end{bmatrix} = \begin{bmatrix}L_1 cos(\theta_1) +L_2 cos(\theta_1+\theta_2)\\ L_1sin(\theta_1) + L_2 sin(\theta_1+\theta_2)\end{bmatrix} \\ \to \begin{bmatrix}\dot x_2 \\ \dot y_2 \end{bmatrix} = \begin{bmatrix} -L_1 sin(\theta_1) -L_2 sin(\theta_1 + \theta_2) & -L_2 sin(\theta_1 + \theta_2) \\ L_1cos(\theta_1) + L_2 cos(\theta_1 + \theta_2) & L_2 cos(\theta_1 + \theta_2) \end{bmatrix} \begin{bmatrix} \dot{\theta}_1 \\ \dot{\theta}_2 \end{bmatrix} \\ \to \\ \mathcal{K}_1=\frac{1}{2}\mathfrak{m}_1(\dot{x}_1^2+\dot{y}_1^2) =\frac{1}{2}\mathfrak{m}_1 L_1^2\dot{\theta}_1^2 \\ \mathcal{K}_2=\frac{1}{2}\mathfrak{m}_2(\dot{x}_2^2+\dot{y}_2^2) =\frac{1}{2}\mathfrak{m}_2 \left( (L_1 ^2 + 2L_1 L_2 cos\theta_2 + L_2^2) \dot{\theta}_1^2 + 2(L_2^2 + L_1 L_2 cos\theta_2)\dot{\theta}_1\dot{\theta}_2 + L_2^2 \dot{\theta}_2^2 \right) \\ \mathcal{P}_1 = \mathfrak{m}_1 g y_1 = \mathfrak{m}_1 g L_1sin\theta_1 \\ \mathcal{P}_2 = \mathfrak{m}_2 g y_2 = \mathfrak{m}_2 g (L_1 sin\theta_1 + L_2 sin(\theta_1+\theta_2)) \\ \mathcal{L}(\theta,\dot{\theta}) = \sum_{i=1}^{2}{(\mathcal{K}_i+\mathcal{P}_i)}\\\]然后,根据L求偏导就ok了…虽然过程的符号有点繁琐,但是步骤非常简单。
\[\tau_1 = \left(\mathfrak{m}_1 L_1^2 + \mathfrak{m}_2(L_1^2+ 2L_1 L_2 cos\theta_2 + L_2^2) \right) \ddot{\theta}_1 \\ +\mathfrak{m}_2 (L_1 L_2 cos\theta_2 + L_2 ^2) \ddot{\theta}_2 - \mathfrak{m}_2 L_1 L_2 sin \theta_2(2 \dot{\theta}_1 \dot{\theta}_2 + \dot{\theta}_2^2) \\ + (\mathfrak{m}_1 + \mathfrak{m}_2)L_1g~cos~{\theta}_1 + \mathfrak{m}_2 g L_2~cos(\theta_1 + \theta_2) \\ ~ \\ \tau_2 = \mathfrak{m}_2 (L_1 L_2~cos~\theta_2 + L_2^2 ) \ddot{\theta}_1 + \mathfrak{m}_2L_2^2 \ddot{\theta}_2 + \mathfrak{m}_2L_1L_2 \dot{\theta}_1^2~sin~\theta_2 + \mathfrak{m}_2 g L_2~cos(\theta_1+\theta_2)\]经过整理,能够整理成以下的形式:
\[\tau = M(\theta)\ddot{\theta} + \underbrace{C(\theta,\dot{\theta}) + G(\theta)}_{h(\theta, \dot{\theta})}\]其中质量矩阵M是对称正定的,C矩阵包含科里奥利力和向心力这俩和速度有关的惯性力,G项则是重力项。
更一般的Lagrange公式
在Lagrange公式中的动能,其实是和质量矩阵M有关的,在后面的Newton-Euler方法中会仔细的介绍这一点,这里作为结论给出:
\[\mathcal{K}(\theta) =\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^n{m_{ij}(\theta)\dot{\theta}_i \dot{\theta}_j} =\frac{1}{2}\dot{\theta}^TM(\theta)\dot{\theta}\]根据这个,再直接代入Lagrange方程,得到N连杆串联机械臂的ID:
\[\tau_i = \sum_{j=1}^{n} \left( m_{ij}(\theta) \ddot{\theta}_j +\sum_{j=1}^{n}\sum_{k=1}^n{\Gamma_{ijk}(\theta)\dot{\theta}_j \dot{\theta}_k} + \frac{\partial \mathcal{P}}{\partial \theta_i} \right)\]恩,其中那个nxnxn的Gamma矩阵中使用了克氏符号(Christoffel symbols),我觉得暂时不懂也是没事的,这里只需要有个概念就行…
\[\tau = M(\theta)\ddot{\theta} + \dot{\theta}^T \Gamma(\theta) \dot{\theta}+ g(\theta) \\ \Gamma_{ijk}(\theta) = \frac{1}{2} \left( \frac{\partial m_{ij}}{\partial \theta_k} + \frac{\partial m_{ik} }{\partial \theta_j} - \frac{\partial m_{jk} }{\partial \theta_i} \right)\]能够明显看出Corilolis 和 centripetal的在每个关节力中的分项是速度的二次型。
对c矩阵中的某一元做进一步分析:
\[c_{ij}(\theta,\dot\theta) = \sum_{k=1}^{n} {\Gamma_{ijk}(\theta) \dot{\theta}_k}\]这里留空等以后来证明这个在机器人控制的稳定性中的作用,尤其是Passivity Property**
结论 8.1:质量矩阵对时间求导减去速度矩阵乘2是反对称阵
证明省略,看书。
\[(\dot{M}-2C)^T=-(\dot{M} - 2C)\]进一步理解质量矩阵
在单质点的动力学中,质量只是一个标量,因此力的大小和对应的加速度方向一致。但是考虑到质量矩阵并不是简单的单位阵,所以\ddot\theta和对应的关节力矩之间存在非线性的映射关系:
沿用之前理解关节速度和末端速度的图形对比方式:
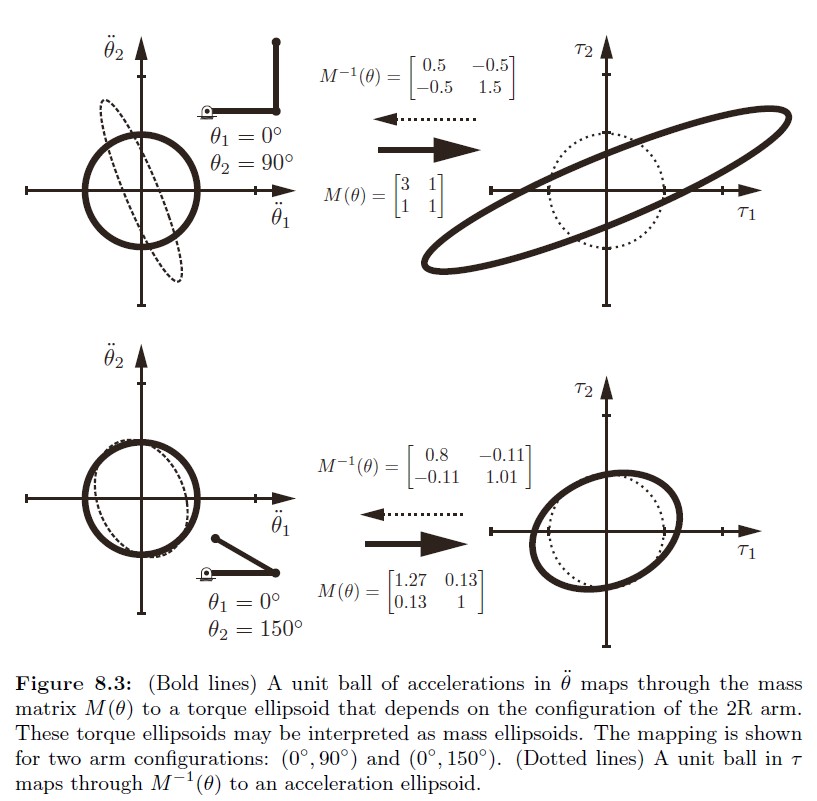
能够看到机器人在不同构型下,加速度和关节力矩的映射关系相差的很多。
等效末端质量矩阵
在实际应用中,一种很常见的情况是拖拽机械臂的末端,那么此时将质量矩阵转换到末端的加速度和对应的力上就比较的形象。仍然利用能量在不同坐标系下的两种表达,V=twist:
\[\frac{1}{2} \dot{\theta}^T M(\theta) \dot{\theta} = \frac{1}{2} \mathcal{V}^T \Lambda(\theta) \mathcal{V} \\\]假设雅克比矩阵是可逆的:
\[\mathcal{V} = J(\theta) \dot{\theta} \\ \mathcal{V}^T \Lambda \mathcal{V} = (J^{-1}\mathcal{V})^TM(J^{-1}\mathcal{V}) \\ =\mathcal{V}^T (J^{-T}MJ^{-1})\mathcal{V} \\\]这样,末端点的质量矩阵就能被转换为Jacobian和关节空间质量矩阵的式子:
\[\Lambda(\theta) = J^{-T}(\theta)M(\theta)J^{-1}(\theta)\]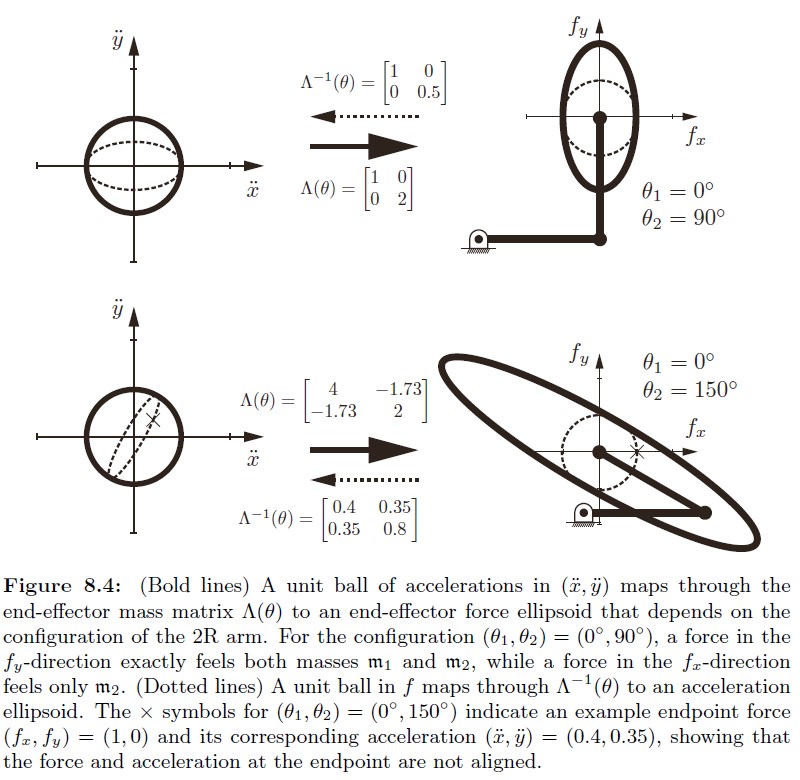
图中第一种情况的等效末端质量矩阵是对角的,可以理解为此时两个方向互不干涉,而第二种情况说明这种构型下末端在某个短轴方向上力很大,速度很小,Jacobian接近奇异(不一定非要关节角打直才奇异,还得看Jacobian的可操作度/条件数)。
Newton-Euler Method(牛顿欧拉迭代法NERA)
刚体动力学(单个刚体)
下面的推导过程主要考虑了刚体的质量分布对质心位置和惯量矩阵的影响,惯量矩阵的中心也是在质心上,因此推导过程的{b}系会放在刚体的质量分布中心。然后推导6维力/力矩关于twist和质量的表达式。

其中每个小质量点的加速度\ddot{p_i}是对速度直接求导得到(\in \R^6),整个刚体的twist是V_b = {\omega_b, v_b}
\[\dot{p}_i=v_b+\omega_b\times p_i \\ \to \ddot{p}_i=\dot{v}_b + \frac{d}{dt}\omega_b \times p_i + \omega_b \times \frac{d}{dt}p_i \\ =\dot{v}_b + \dot{\omega}_b\times p_i + \omega_b \times (v_b + \omega_b \times p_i) \\ =\dot{v}_b+[\dot{\omega}_b]r_i + [\omega_b]v_b+[\omega_b]^2r_i\]吐槽一下这里的符号,力矩是小写m,而质量对应的是花体的m。
对叉乘的化简还是用了性质:
\[[a]=-[a]^T \\ [a]b = a\times b = -b\times a = -[b]a \\ [a][b] = ([b][a])^T = [a]^T [b]^T = (-[a])(-[b])\]同时还用到质心的定义:
\[\sum_i{m_i r_i} = 0 \to \sum_i{m_i[r_i]} = 0I(矩阵分量求和都是0)\]于是就能导出图片中6维F向量的公式:
\[\mathcal{F}_b=\begin{bmatrix}m_b \\f_b \end{bmatrix} =\begin{bmatrix}\mathcal{I}_b \dot{\omega}_b + [\omega_b]\mathcal{I}_b \omega_b \\ \mathfrak{m}(\dot{b}_b + [\omega_b]v_b) \end{bmatrix} \\ \mathcal{I}_b = -\sum_i{\mathfrak{m}_i[r_i]^2}\]这里的惯量\mathcal{I}也是对称正定的。并且只要坐标系固定,惯量矩阵就是固定的(只和质量分布有关),展开[r_i]可以得到
\[\mathcal{I}_b= \begin{bmatrix} \sum{\mathfrak{m}_i(y_i^2+z_i^2)} & -\sum{\mathfrak{m}_i x_i y_i} &-\sum{\mathfrak{m}_i x_i z_i} \\ -\sum{\mathfrak{m}_i x_i y_i} & \sum{\mathfrak{m}_i (x_i^2+z_i^2)}&-\sum{\mathfrak{m}_i y_i z_i} \\ -\sum{\mathfrak{m}_i x_i z_i} & -\sum{\mathfrak{m}_i y_i z_i} & \sum{\mathfrak{m}_i (x_i^2+y_i^2)}\\ \end{bmatrix}\]如果有密度的话就按照密度三重积分(dV),对惯量矩阵求特征值和特征向量能够得到惯量的主轴。一般坐标系会沿着那个建,或者是对称物体的话,主轴也是在对称轴上,此时交叉项都为0.
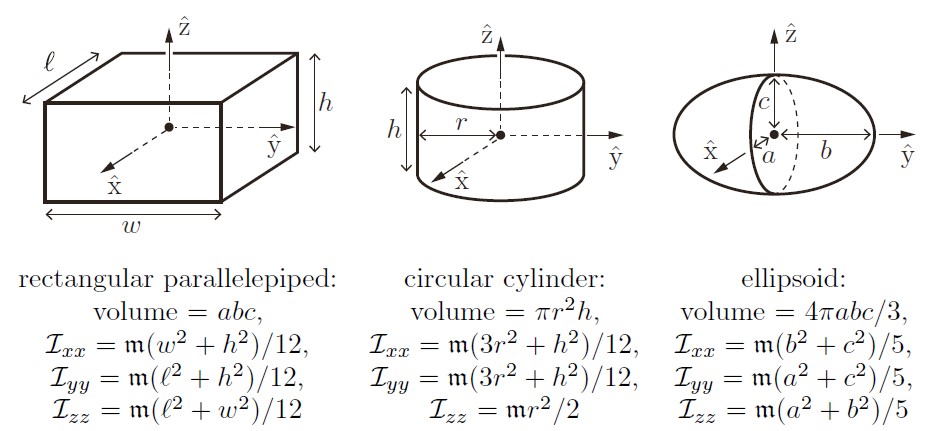
上图为常用几何体惯量计算公式。
坐标系的旋转和平移变换会导致惯量矩阵的变化
旋转:{c}系相对{b}系有个旋转
\[\frac{1}{2} \omega_c^T \mathcal{I}_c \omega_c =\frac{1}{2} \omega_b^T \mathcal{I}_b \omega_b \\ =\frac{1}{2} (R_{bc}\omega_c)^T \mathcal{I}_b(R_{bc} \omega_c ) \\ =\frac{1}{2} \omega_c^T (R_{bc}^T \mathcal{I}_b R_{bc}) \omega_c \\ \to \mathcal{I}_c = R_{bc}^T \mathcal{I}_b R_{bc}\]平行轴定理:坐标轴平行,但是{q}原点在{b}中的坐标为q = (qx,qy,qz)^T
\[\mathcal{I}_q=\mathcal{I}_b + \mathfrak{m}(q^TqI - qq^T)\\ = \begin{bmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{bmatrix} + \mathfrak{m} \begin{bmatrix} q_y^2 + q_z^2 & -q_x q_y &-q_x q_z \\ -q_y q_x & q_x^2 + q_z^2 & -q_y q_z \\ -q_z q_x & -q_z q_y & q_x^2 + q_y^2 \end{bmatrix}\]平行轴定理只是其中的一种特殊情况。
刚体的Twist-Wrench关系
整理之前的Wrench和Twist的关系:
\[\mathcal{F}_b=\begin{bmatrix}m_b \\ f_b\end{bmatrix} = \underbrace{\begin{bmatrix}\mathcal{I}_b & 0\\ 0 & \mathfrak{m}I \end{bmatrix}} _{spatial~inertial~matrix~\mathcal{G}_b} \begin{bmatrix}\dot\omega_b \\ \dot{v}_b\end{bmatrix} + \begin{bmatrix}[\omega_b] & 0\\ 0 & [\omega_b] \end{bmatrix} \begin{bmatrix}\mathcal{I}_b & 0\\ 0 & \mathfrak{m}I \end{bmatrix} \underbrace{\begin{bmatrix}\omega_b \\ v_b\end{bmatrix}}_{Twist~\mathcal{V}_b}\]这时,我们可以用spatial vector表示刚体的动能:
\[kinetic~energy =\frac{1}{2}\mathcal{V}_b^T\mathcal{G}_b \mathcal{V}_b\]空间的动量(spatial momentum)表示为:
\[\mathcal{P}_b=\begin{bmatrix} \mathcal{I}_b \omega_b \\ \mathfrak{m}v_b \end{bmatrix} =\mathcal{G}_b \mathcal{V}_b\]又有 v x v = 0, [v]^T=-[v],这步操作是有意义的…(Twist 的 cross-product, Lie Bracket)
\[\mathcal{F}_b=\begin{bmatrix}m_b \\ f_b\end{bmatrix} = \begin{bmatrix}\mathcal{I}_b & 0\\ 0 & \mathfrak{m}I \end{bmatrix} \begin{bmatrix}\dot\omega_b \\ \dot{v}_b\end{bmatrix} - \begin{bmatrix}[\omega_b] & 0\\ [v_b] & [\omega_b] \end{bmatrix}^T \begin{bmatrix}\mathcal{I}_b & 0\\ 0 & \mathfrak{m}I \end{bmatrix} \begin{bmatrix}\omega_b \\ v_b\end{bmatrix}\\ =\mathcal{G}_b\dot{\mathcal{V}}_b - [ad_{\mathcal{V}_b}]^T(\mathcal{P}_b)\]定义8.3 Lie Bracket
给定两个twist,他们的Lie Bracket 写作:[ad_{V_1}]V_2或者ad_{V_1}(V_2)定义如下:
这里的[ad(twist)] 和之前的Adjoint(写作[Ad_{T}])很不一样!
\[[Ad_T] = \begin{bmatrix}R & 0 \\ [p]R & R \end{bmatrix} \in R^{6\times6} \\ \begin{bmatrix} [\omega_1] & 0 \\ [v_1] & [\omega_1] \end{bmatrix} \begin{bmatrix} \omega_2 \\ v_2 \end{bmatrix} = [ad_{\mathcal{V}_1}]\mathcal{V}_2=ad_{\mathcal{V}_1}(\mathcal{V}_2) \\ [ad_{\mathcal{V}}] = \begin{bmatrix} [\omega_1] & 0 \\ [v_1] & [\omega_1] \end{bmatrix} \in R^{6\times6}\]证明思路
\[we~have~[\omega_1 \times \omega_2] = [\omega_1][\omega_2] - [\omega_2][\omega_1]\in so(3)\\ [\mathcal{V}_1\times \mathcal{V}_2]_{Lie~Bracket} = [\mathcal{V}_1][\mathcal{V}_2]-[\mathcal{V}_2][\mathcal{V}_1] \in se(3)\\ = \begin{bmatrix}[\omega_1] & v_1 \\ 0 & 0\end{bmatrix} \begin{bmatrix}[\omega_2] & v_2 \\ 0 & 0\end{bmatrix} -\begin{bmatrix}[\omega_2] & v_2 \\ 0 & 0\end{bmatrix} \begin{bmatrix}[\omega_1] & v_1 \\ 0 & 0\end{bmatrix}\\ =\begin{bmatrix}[\omega_1][\omega_2]-[\omega_2][\omega_1] & [\omega_1]v_2-[\omega_2]v_1 \\ 0 & 0\end{bmatrix}\\ =\begin{bmatrix}[\omega'] & v' \\ 0 & 0\end{bmatrix}\]根据skew矩阵的性质,比较可以得出:
\[\mathcal{V}_1 \times \mathcal{V}_2 = \mathcal{V'} \\ [\omega'] = [\omega_1][\omega_2]-[\omega_2][\omega_1]=[\omega_1\times \omega_2]\to\omega'=\omega_1 \times \omega_2=[\omega_1]\omega_2 \\ v'=[\omega_1]v_2-[\omega_2]v_1=[v_1]\omega_2 + [\omega_1]v_2 \\ \to\mathcal{V'}=\begin{bmatrix}\omega' \\v' \end{bmatrix} =\begin{bmatrix} [\omega_1] & 0 \\ [v_1] & [\omega_1] \end{bmatrix} \begin{bmatrix} \omega_2 \\ v_2 \end{bmatrix}=[ad_{\mathcal{V}_1}]\mathcal{V}_2\]有了Lie Bracket之后,就能更加简洁的表示力与spatial inertia matrix和spatial velocity的关系了。
Little Add V1 times V2 is the Lie Bracket of V1 and V2, which is the acceleration measuring how motion along the twist V2 would change the body follows the V1.
然后我们搞了这么多到底是为了什么呢?!
这个式子将之前3X3的惯量矩阵,3维速度,角速度以及3x3的cross bracket 换成了6x6的spatial inertia 矩阵,和twist以及6x6的lie bracket。
当坐标系发生变化时,我们能写出在另一个坐标系{a}下的F_a的表达式:
\[kinetic~energy\to\frac{1}{2}\mathcal{V}_a^T\mathcal{G}_a\mathcal{V}_a =\frac{1}{2}\mathcal{V}_b^T\mathcal{G}_b\mathcal{V}_b\\ =\frac{1}{2}([Ad_{T_{ba}}]\mathcal{V}_a)^T\mathcal{G}_a[Ad_{T_{ba}}]\mathcal{V}_a \\ =\frac{1}{2}\mathcal{V}_a^T \underbrace{[Ad_{T_{ba}}]^T\mathcal{G}_a[Ad_{T_{ba}}]}_{\mathcal{G}_a} \mathcal{V}_a \\ \to \mathcal{F}_a=\mathcal{G}_a\dot{\mathcal{V}}_a - [ad_{\mathcal{V}_a}]^T(\mathcal{G}_a\mathcal{V}_a)\]对于单刚体的FD可以写作:
\[\dot{\mathcal{V}}_b=\mathcal{G}_b^{-1}(\mathcal{F}_b + [ad_{\mathcal{V}_b}]^T(\mathcal{G}_b\mathcal{V}_b))\]之后的RNEA(recursive Newton-Euler algorithm)主要还是根据这个式子进行下一步的推导。
RNEA
基本的思想看 Lynch这本书就够了,感觉讲的比Featherstone更加清楚。
符号定义
每个连杆i的坐标系(body-fixed reference frame){i}固定在各自的质心上,base frame记做{0},末端的坐标系记做{n+1},并且固定在{n}上。
记机器人在零位时的configuration下,各个link之间的变换关系:{j}在{i}下的矩阵M_{i,j} \in SE(3),第i个link在基坐标系{0}下的矩阵记做M_i。
\[M_{i-1,i}=M_{i-1}^{-1}M_i\]零位下,第i个joint运动对应的screw axis在{i}系下记做A_i,同时在{0}系下记做S_i
\[\mathcal{A}_i=Ad_{M_i^{-1}}(\mathcal{S}_i)\]在运动过程中,定义T_{i,j}\inSE(3) 作为{j}在{i}系下的位型,因为是和\theta有关系的,所以:
\[T_{i-1,i}(\theta_i)=M_{i-1,i}e^{[A_i]\theta_i} \\ T_{i,i-1}(\theta_i)=e^{-[A_i]\theta_i} M_{i,i-1}\\\]在计算过程中的符号定义如下:
- link-i的twist在{i}下看记做V_i=(\omega_i, v_i)
- joint-i产生的wrench传导到frame-i,在{i}下记做F_i=(m_i,f_i)
- 记第i个link的spatial inertia matrix在{i}下为G_i \in R^{6x6},因为frame已经建在质心上,所以G_i是个块对角阵。
根据以上,能够进行牛顿欧拉的前向和后向迭代:
从base->End:
根据前一个关节的twist和坐标变换关系,以及下一个link绕轴的转动可以计算下一个link自身坐标系下的twist:
\[\mathcal{V}_i=\mathcal{A}_i\dot{\theta}_i + [Ad_{T_{i,i-1}}]\mathcal{V}_{i-1}\]对上面等式求导:
\[\dot{\mathcal{V}}_i = \mathcal{A}_i\ddot{\theta}_i+[Ad_{T_{i,i-1}}]\dot{\mathcal{V}}_{i-1} +\frac{d}{dt}\left([Ad_{T_{i,i-1}}]\right) \mathcal{V}_{i-1}\]其中,对Ad矩阵求导的部分可以化简为:
\[\frac{d}{dt}\left([Ad_{T_{i,i-1}}]\right) \mathcal{V}_{i-1} =\frac{d}{dt}\left( \begin{bmatrix} R_{i,i-1} & 0 \\ [p]R_{i,i-1} & R_{i,i-1} \end{bmatrix} \right) \mathcal{V}_{i-1} \\ = \begin{bmatrix} [\hat\omega(-\dot{\theta}_i)]R_{i,i-1} & 0 \\ [\hat{v}(-\dot{\theta}_i)]R_{i,i-1} - [\hat\omega(-\dot{\theta}_i)][p]R_{i,i-1} & [\omega(-\dot{\theta}_i)]R_{i,i-1} \end{bmatrix} \mathcal{V}_{i-1} \\ = \underbrace{ \begin{bmatrix} -[\hat{\omega}\dot{\theta}_i ] & 0 \\ -[\hat{v}\dot{\theta}_i ] & -[\hat{\omega}\dot{\theta}_i ] \\ \end{bmatrix} }_{-[ad_{\mathcal{A}_i \dot{\theta}_i}]} \underbrace{ \begin{bmatrix} R_{i,i-1} & 0 \\ [p]R_{i,i-1} & R_{i,i-1}\\ \end{bmatrix} }_{[Ad_{T_{i,i-1}}]} \mathcal{V}_{i-1}\\ = -[ad_{\mathcal{A}_i\dot{\theta}_i}]\mathcal{V}_i \\ = [ad_{\mathcal{V}_i}]\mathcal{A}_i\dot{\theta}_i\]至此,能够从{0}计算到末端{n}的V,\dotV,并且根据前面F和G,V,\dotV的关系:
再根据后向迭代,从{n}的wrench开始一直计算到{0}的wrench,顺便能计算每个Joint的力矩:
\[\mathcal{G}_i \dot{\mathcal{V}}_i-ad_{\mathcal{V}_i}^T(\mathcal{G}_i\mathcal{V}_i) =\mathcal{F}_i-Ad_{T_{i+1,i}}^T(\mathcal{F}_{i+1}) \\ \tau_i=\mathcal{F}_i^T \mathcal{A}_i\]在最终迭代过程中,\dot{V{0}}的初值设置为(0,-g),同时末端的wrench是F{n+1}
算法
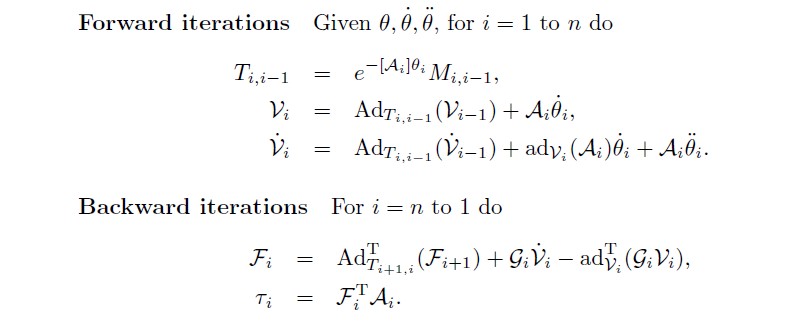
动力学方程的解析表达式
这一部分暂时略过…因为实际中还是用迭代计算的比较多,一次性把M,C,G矩阵都存起来没有什么意义…
REFERENCE
[1] http://www.terriex.com/index.php/archives/21/